

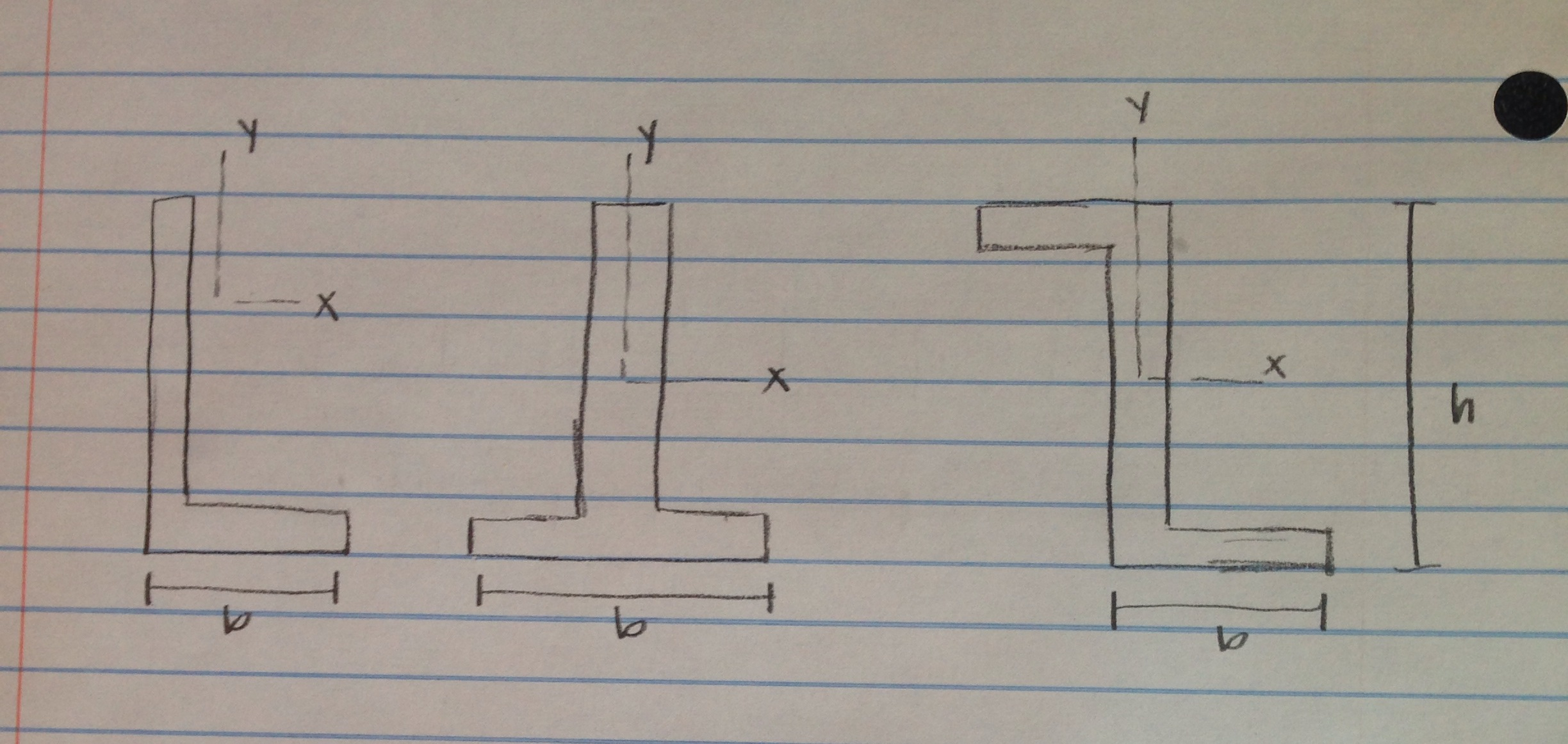
Moment of Inertia has the same relationship to angular acceleration as mass has to linear acceleration. calculate the moment of inertia about specified axis, centroid about specified axis, section modulus. Mass Moment of Inertia (Moment of Inertia) - I - is a measure of an object's resistance to change in rotation direction. It is a common structural engineering convention that B refers to the width of the rectangle, parallel to a. Where the xx and yy refer to the particular axis, or direction, being considered.
#Ixx moment of inertia formula how to
Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I. Moment of Inertia of a square formula I a 4 12. The general formula used when determining how to find the moment of inertia of a rectangle is: Ixx BD3 12,Iyy B3D 12 I x x B D 3 12, I y y B 3 D 12. Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Where Ixy is the product of inertia, relative to centroidal axes x,y, and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_.

Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape (=bh in case of a rectangle).įor the product of inertia Ixy, the parallel axes theorem takes a similar form: The so-called Parallel Axes Theorem is given by the following equation: Welcome to our calculator for the moment of inertia for an angle section about its centroidal axes as well as about its base. Ixx, Iyy, and Izz mass moments of inertia of body about the x,y, and I axes, respectively. I xx H 3 b/12 + 2 h 3 B/12 + hB (h+H) 2 /4 Area moment of inertia. The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. C Channel Area Moment of Inertia Formula.


 0 kommentar(er)
0 kommentar(er)
